Calculate a parabola from three known points

I was looking for a quick fix for calculating values along a parabola given three known points. Scouting around I found a nice symbolic C function doing exactly what I wanted (see here). The function doing the work of finding your unknowns is:

 
	def calc_parabola_vertex(x1, y1, x2, y2, x3, y3):
		'''
		Adapted and modifed to get the unknowns for defining a parabola:
		http://stackoverflow.com/questions/717762/how-to-calculate-the-vertex-of-a-parabola-given-three-points
		'''

		denom = (x1-x2) * (x1-x3) * (x2-x3);
		A     = (x3 * (y2-y1) + x2 * (y1-y3) + x1 * (y3-y2)) / denom;
		B     = (x3*x3 * (y1-y2) + x2*x2 * (y3-y1) + x1*x1 * (y2-y3)) / denom;
		C     = (x2 * x3 * (x2-x3) * y1+x3 * x1 * (x3-x1) * y2+x1 * x2 * (x1-x2) * y3) / denom;

		return A,B,C

By defining our three known xy points, we can use the above function to find the values of the unknowns a, b and c which would satisfy the equation of y = ax² + bx + c:

 
	#Define your three known points
	x1,y1=[2,11]
	x2,y2=[-4,35]
	x3,y3=[0,-5]

	#Calculate the unknowns of the equation y=ax^2+bx+c
	a,b,c=calc_parabola_vertex(x1, y1, x2, y2, x3, y3)

We now have our full equation and can apply it to calc values along the parabola:

 
	#Define x range for which to calc parabola
	import numpy as np

	x_pos=np.arange(-30,30,1)
	y_pos=[]

	#Calculate y values 
	for x in range(len(x_pos)):
		x_val=x_pos[x]
		y=(a*(x_val**2))+(b*x_val)+c
		y_pos.append(y)

And then to plot it we can just do this:

 
# Plot the parabola (+ the known points)
	import matplotlib.pyplot as plt

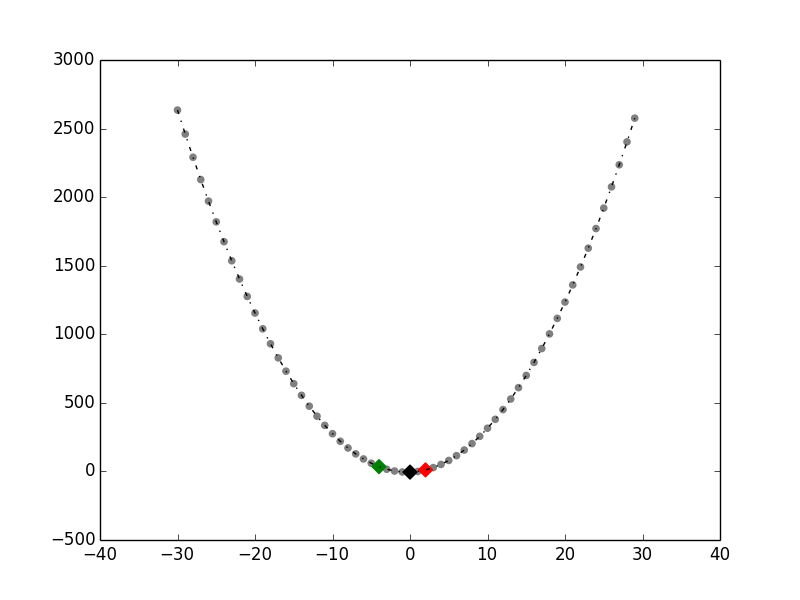
	plt.plot(x_pos, y_pos, linestyle='-.', color='black') # parabola line
	plt.scatter(x_pos, y_pos, color='gray') # parabola points
	plt.scatter(x1,y1,color='r',marker="D",s=50) # 1st known xy
	plt.scatter(x2,y2,color='g',marker="D",s=50) # 2nd known xy
	plt.scatter(x3,y3,color='k',marker="D",s=50) # 3rd known xy
	plt.show()

…which gives us this:

Parabola from our three known points

Written on November 16, 2015