A component of a signal can easily be removed by using the Fast Fourier Transform (and its inverse) - in Python, this is easily implemented using numpy. The code below zeros out parts of the FFT - this should be done with caution and is discussed in the various threads you can find here. Martin put together a function to smooth the FFT (based on Moisan, 2011) which can help with this here.

A simple example (take from here):

import numpy as np
import matplotlib.pyplot as plt

# Make some data
t=np.linspace(0,1,256, endpoint=False)
x = np.sin(2 *np.pi * 3 * t) + np.cos(2 * np.pi * 100 * t)

# Run FFT
X=np.fft.fft(x)

# Zero some channels
X[64:192] = 0

# Run inverse FFT
y = np.fft.ifft(X)

# Plot it
plt.plot(x)
plt.plot(y)
plt.legend(['raw signal', 'filtered signal'])
plt.show(block=False)

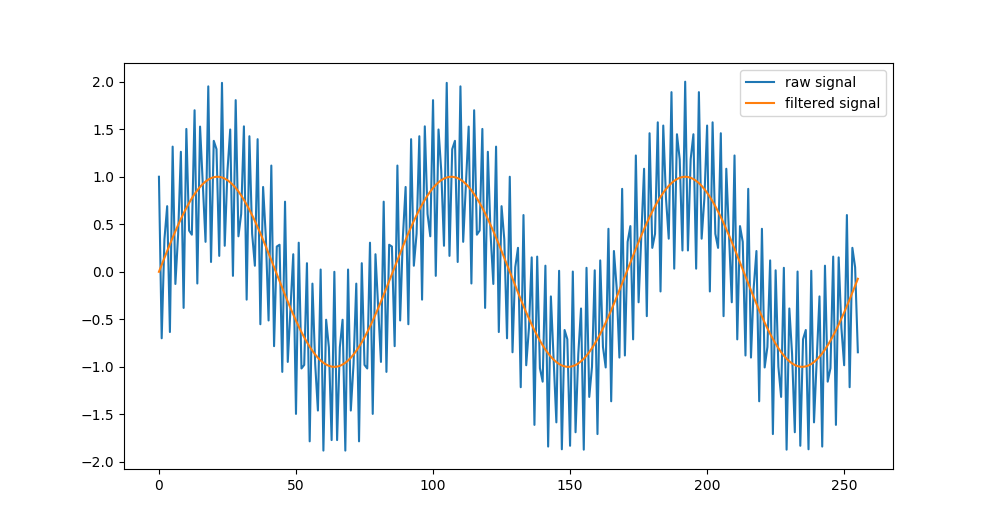
What we’ve done is

• run FFT on a signal
• zero out some of the bins (real and complex)
• run an inverse FFT on the remaining
• returned the signal, without the components you zeroed