3D plotting with matplotlib
There are a number of options available for creating 3D like plots with matplotlib. Let’s get started by first creating a 3d scatter plot.
3D scatter plot
Let’s first create some data:
import numpy as np
xyz=np.array(np.random.random((100,3)))
and assign it to specific variables (for clarity and also to modify the z values):
x=xyz[:,0]
y=xyz[:,1]
z=xyz[:,2]*100
Now we need to import the 3d package:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
To create our 3D plot, we must take a slightly different approach which will provide us with greater opportunity for plot customisation. First we will create and assign a figure object:
fig = plt.figure()
Now, from the figure object we are going to create a subplot (of which there will only be one) - the need to do this is to ensure that we have specific access to the properties of the figure we are creating (before, where we called say plt.scatter() we were unable to specifically access its axis properties other than by default):
ax = fig.add_subplot(111, projection='3d')
We will revisit what is meant by the 111 later on in the multiple plots section. For now, have a look at the number of options now available to you for modifying the axis object by typing ax. followed by the tab key.
The 3D scatter plotting function (Axes3D.scatter()) takes in x, y and z values which we can set using our xyz array object:
ax.scatter(x,y,z)
which we can then show (or even save) as normal - have a go at interacting with the figure that pops up:
plt.show()
To add a colorbar, we need to assign the definition of the scatter plot to a variable which we then pass to the colorbar function. First, re-assign the figure and axis variables:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
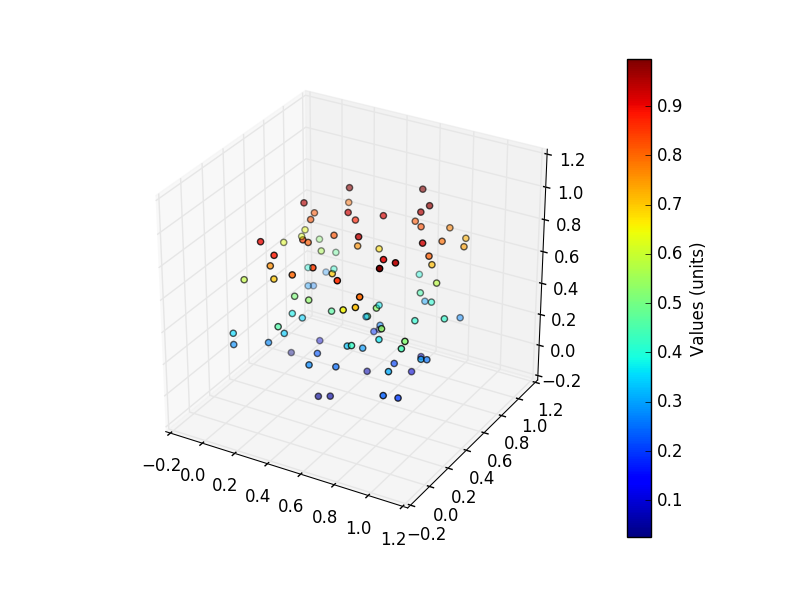
Now recreate the scatter plot and assign it ot a variable name (we call ours pnt3d) - to make the colorbar work, you must also set the c option - as we are using our z variable to colour our pioints, we set this as c=z:
pnt3d=ax.scatter(x,y,z,c=z)
Now create your colorbar, and pass in the scatter plot (called pnt3d):
cbar=plt.colorbar(pnt3d)
Using the colorbar object (cbar), we can also give it a title:
cbar.set_label("Values (units)")
We can then plot this as normal:
plt.show()
and you should end up with something like this:
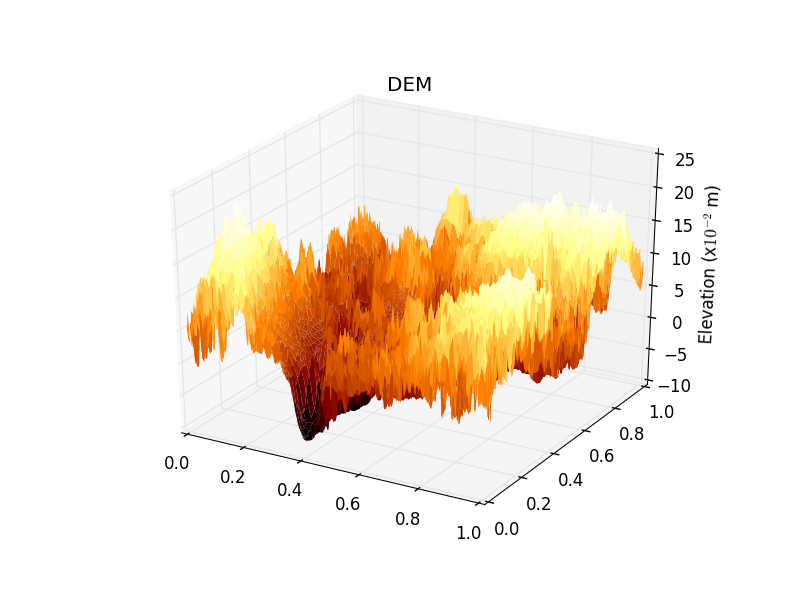
3D surface plot
To make a 3D surface plot, we can reuse the dem we opened before (which you can save using this link).
Read this in as a numpy array using scipy.misc.imread:
from scipy import misc
dem=misc.imread('/path/to/dem.tif')
The function to plot 3d surfaces is available as for the 3d scatter plot demonstrated above - it can be imported as follows:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
Notice that we have set an alias for each of the imports - plt for matplotlib.pyplot and Axes3D for mpl_toolkits.mplot3d.
If you have a look at the documentation for mpl_toolkits.mplot3d.plot_surface (which you can access using your alias by typing Axes3D.plot_surface?), you will see that it takes in x, y and z values that must all be 2D arrays - the problem at the moment is that your surface array (dem) only provides the z data - you don’t have the x or y components.
To create this, we can use a function from numpy called meshgrid. For a given array of values, the meshgrid function creates 2 equally sized grids that represent the x and y location at each element of the array, that is to say that for an element in our dem array, the x and y mesh grids will provide information of its location in x and y space… let’s try an example…
First, check on the shape of your dem array:
>>> dem.shape
>>> (592L, 584L)
Now import numpy - we’ll give it an alias of np):
import numpy as np
Now we need to create the dimensions of what will be our mesh grids of x and y. First assign the dimensions of the dem array to variables of nx and ny:
ny, nx = dem.shape
The above statement assigns the two values returned by the dem.shape call to the two variables nx and ny.
We now need to make two lists of values ranging from 0 to the maximum length of the image in both the x and y dimensions - we can do this by using numpy’s linspace function:
x = np.linspace(0, 1, nx)
y = np.linspace(0, 1, ny)
This has created every likely element position in the x and y dimensions - remember that for a given column, the x value will remain the same (now matter how far up or down the column it is) and the same for y in the horizontal direction - if this doesn’t make sense, we’ll have an image to look at in a minute.
Now we just need to pass in the x and y variables to np.meshgrid() to get our arrays of x and y position (calling the resultant grids xv and yv):
xv, yv = np.meshgrid(x, y)
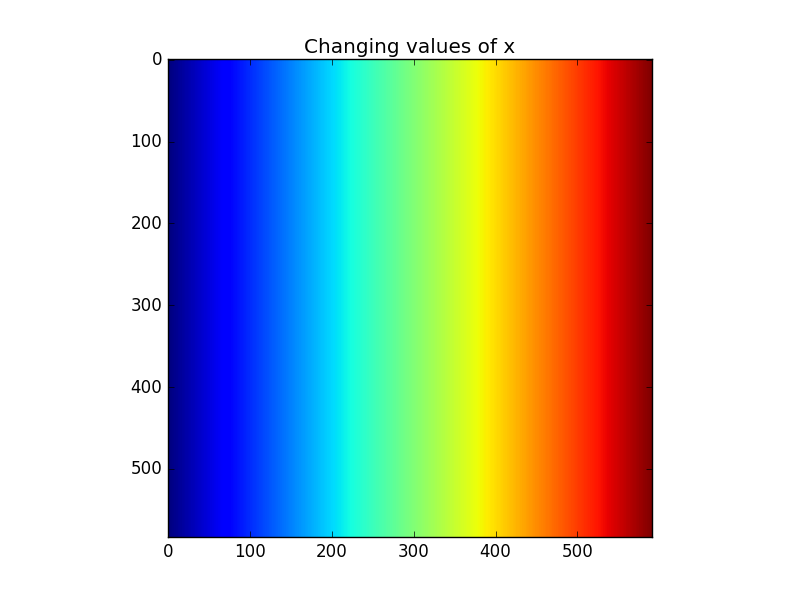
To visualise these grids, here is x, the values of which only change from left to right:
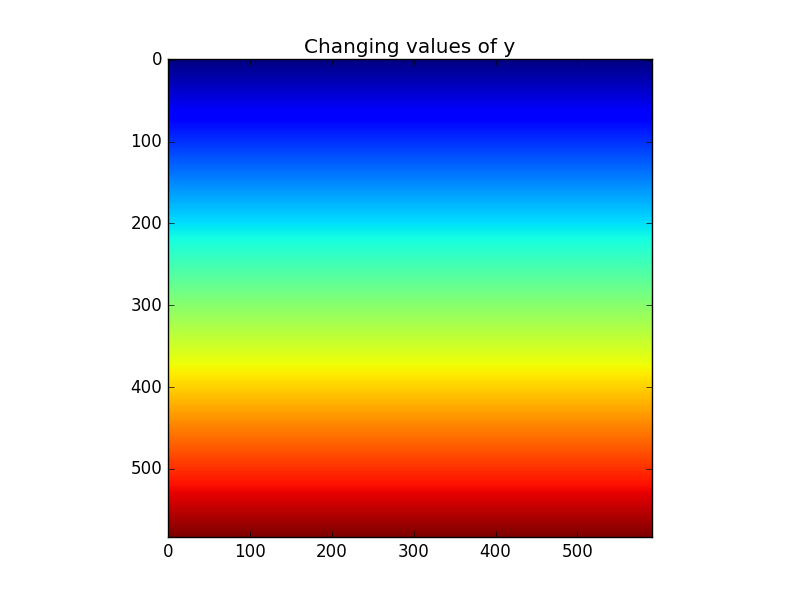
and here is y, the values of which only change from top to bottom:
The key point now is that we have 3 2d arrays, representing x, y and z, held by the variables xv, yv and dem respectively. Now we can pass these into the Axes3D.surface_plot(). We have to do this in the same way as for the 3d scatter plot above, so type:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
dem3d=ax.plot_surface(xv,yv,dem)
plt.show()
To adjust the colours, set the type of colormap you want to use using the cmap option when creating the main plot:
dem3d=ax.plot_surface(xv,yv,dem,cmap='afmhot')
You might also want to add a title and axis labels to the plot - as we are using a specific call to the plot axis, we must set this using:
ax.set_title('DEM')
ax.set_zlabel('Elevation (m)')
You can then view it using:
plt.show()
If you prefer a smoother looking image, then you want to adjust the linewidth option when creating the plot:
dem3d=ax.plot_surface(xv,yv,dem,cmap='afmhot', linewidth=0)
You might also like to play with the alpha option which changes transparency:
dem3d=ax.plot_surface(xv,yv,dem,cmap='afmhot', linewidth=0, alpha=0.2)
If you want to change the scale of the values in the dem array, then you are best modifying the values before plotting it e.g.:
dem_100=dem/100
Remember that if you make these changes, you need to then recreate the figure and axis instances. So, after making some additional changes, we create the figure by typing:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
dem3d=ax.plot_surface(xv,yv,dem_100,cmap='afmhot', linewidth=0)
ax.set_title('DEM')
ax.set_zlabel('Elevation (x$10^{-2}$ m)')
plt.show()
Your plot should look something like this: